已知，P为等边三角形内一点
未命名 | 2017年10月24日09:31:01 | 阅读：326 | 评论：2
简介：
已知，P为等边三角形内一点，且BP=3，PC=4，将BP绕点B顺时针旋转60°至BP’的位置．（1）试判断△BPP’的形状，并说明理由；（2）若∠BPC=150°，求PA．
已知，P为等边三角形内一点，且BP=3，PC=4，将BP绕点B顺时针旋转60°至BP’的位置．（1）试判断△BPP’的形状，并说明理由；（2）若∠BPC=150°，求PA．
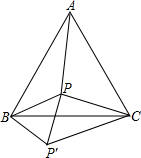（1）△BPP’是等边三角形．
理由：∵BP绕点B顺时针旋转60°至BP′，
∴BP=BP′，∠PBP=60°；
∴△BPP′是等边三角形．
（2）∵△BPP′是等边三角形，
∴∠BPP′=60°，PP'=BP=3，∠P'PC=∠BPC-∠BPP=150-60°=90°；
在Rt△P'PC中，由勾股定理得P'C==5，
∴PA=P′C=5．
温馨提示：本文是作者 panpan39 的原创文章，转载请注明出处和附带本文链接！
下一篇：圆的定义，高视角看圆
相关文章
六班网
www.6ban.cn
- 最近发表
- 标签列表
- 搜索
