二次函数经典题目：二次函数y=ax2+bx+c（a≠0）

二次函数y=ax²+bx+c（a≠0）的图象过点（-1，2），且与x轴交点的横坐标为x₁、x₂，其中-2＜x₁＜-1，0＜x₂＜1，则下列结论： ①4a-2b+c＜0，②2a-b<0，③a+c<1，④b²+8a＞4ac．其中正确的是______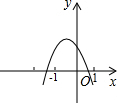． 解析：∵图象开口向下，则a＜0， ∵图象对称轴在y轴左侧，则a，b同号，即b＜0， 图象与y轴交于y轴正半轴，故c＞0， 当x=-2时，函数值小于0， 即4a-2b+c＜0，故①正确； 由-2＜x₁＜-1，0＜x₂＜1，可知对称轴x>-1 ∴2a＜b，即2a-b＜0， ②正确 ③开始尝试用c/a，x1*x2最大为0，最小-2，探索未果 利用特值：根据-2＜x₁＜-1，0＜x₂＜1，可以估算出两根的值， 例如x₁=-1.5，x₂=0.5，图象还经过点（-1，2），得出函数的解析， 解得：a=-8/3＜-1，b=-8/3, c=2  a+c<0 ④b²+8a＞4ac． 根据③中计算结果，可以得出：b²+8a＞4ac， 故④b²+8a<4ac，不正确． 也可以这么算 ： 将点（-1，2）代入y=ax²+bx+c中，得a-b+c=2，即c=2-a+b， 由2a-b＜0，则（2a-b）²＞0， 即b²＞-4a²+4ab， ∴b²+8a＞8a-4a²+4ab=4a（2-a+b）=4ac， 故选：C．