已知三个实数a，b，c满足a﹣2b+c＝0，a+2b+c＜0

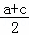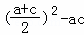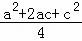已知三个实数a，b，c满足a﹣2b+c＝0，a+2b+c＜0，则（　　） A．b＞0，b²﹣ac≤0                      B．b＜0，b²﹣ac≤0 C．b＞0，b²﹣ac≥0                      D．b＜0，b²﹣ac≥0 D【分析】根据a﹣2b+c＝0，a+2b+c＜0，可以得到b与a、c的关系，从而可以判断b的正负和b²﹣ac的正负情况，本题得以解决． 【解答】解：∵a﹣2b+c＝0，a+2b+c＜0， ∴a+c＝2b，b＝， ∴a+2b+c＝（a+c）+2b＝4b＜0， ∴b＜0， ∴b²﹣ac＝＝﹣ac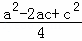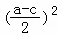＝＝≥0， 即b＜0，b²﹣ac≥0， 故选：D．