网站首页 >> 未命名 >> 正文

如图，在平行四边形ABCD中，AD＞AB．

未命名 | 2014年05月21日12:36:04 | 阅读：497 | 评论：17

简介： 如图，在平行四边形ABCD中，AD＞AB．(1)作出∠ABC的平分线(尺规作图，保留作图痕迹，不写作法)； (2)若(1)中所作的角平分线交AD于点E，AF⊥BE，垂足为点O，交BC于点F，连接EF
如图，在平行四边形ABCD中，AD＞AB．(1)作出∠ABC的平分线(尺规作图，保留作图痕迹，不写作法)； (2)若(1)中所作的角平分线交AD于点E，AF⊥BE，垂足为点O，交BC于点F，连接EF．求证：四边形ABFE为菱形． 解：（1）如图所示： [caption id="attachment_405" align="alignnone" width="242"]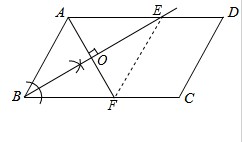如图，在平行四边形ABCD中，AD＞AB． 如图，在平行四边形ABCD中，AD＞AB．[/caption] （2）证明：∵BE平分∠ABC， ∴∠ABE=∠FBE， ∵∠EBF=∠AEB， ∴∠ABE=∠AEB， ∴AB=AE， ∵AO⊥BE， ∴BO=EO， ∵在△ABO和△FBO中， ∠ABO＝∠FBO BO＝BO ∠AOB＝∠BOF ∴△ABO≌△FBO（ASA）， ∴AO=FO， ∵AF⊥BE，BO=EO，AO=FO， ∴四边形ABFE为菱形． 解析：此题主要考查了角平分线的作法以及菱形的判定和全等三角形的判定与性质，熟练掌握菱形的判定是解题关键． （1）根据角平分线的作法作出∠ABC的平分线即可； （2）首先根据角平分线的性质以及平行线的性质得出∠ABE=∠AEB，进而得出△ABO≌△FBO，进而利用AF⊥BE，BO=EO，AO=FO，得出即可． 知识点关键词：菱形的判定；平行四边形的性质；作图—基本作图．

温馨提示：本文是作者 panpan39 的原创文章，转载请注明出处和附带本文链接！

上一篇：

下一篇：

相关文章

网友点评

  • 梦想成真

    梦想成真

    2014-09-14 14:25:50    回复

    帮忙算一下 一个直角三角形，它们的角度各是90° 67.5 ° 22.5° 底边长度刚好1米，求其他两条边

  • 赵炎

    赵炎

    2014-10-25 13:38:30    回复

    我家孩子数学不怎么好，这可怎么办。

    • panpan39

      panpan39

      2014-10-25 21:28:32    回复

      请问家长，您孩子是小学还是初中?

  • 。。

    。。

    2014-10-26 20:25:35    回复

    谁知道今年数学八年级上月考卷子，急———

  • 学习帮手网网友

    学习帮手网网友

    2014-09-14 14:25:50    回复

    帮忙算一下 一个直角三角形，它们的角度各是90° 67.5 ° 22.5° 底边长度刚好1米，求其他两条边

本文已有17位网友发表了点评 - 欢迎您

六班网

六班网

www.6ban.cn

最近发表
网站分类
标签列表
搜索
sitemap 丨网站地图

Copyright @ 2019-2021 六班数学网 All Rights Reserved.

本站所发表的文章版权归作者所有，转载或抄袭他人作品，带来的后果与本站无关。若存在您非授权的原创作品，请第一时间联系本站删除

切换白天模式 切换夜间模式 白天返回顶部 夜间返回顶部