如图，分别以直角△ABC的斜边AB,，直角边AC为边

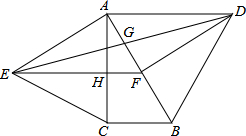
如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论： ①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=1/4BD 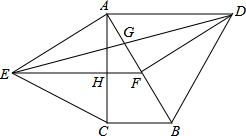其中正确结论的为------（请将所有正确的序号都填上） 解：∵△ACE是等边三角形， ∴∠EAC=60°，AE=AC， ∵∠BAC=30°， ∴∠FAE=∠ACB=90°，AB=2BC， ∵F为AB的中点， ∴AB=2AF， ∴BC=AF， ∴△ABC≌△EFA， ∴FE=AB， ∴∠AEF=∠BAC=30°， ∴EF⊥AC，故①正确， ∵EF⊥AC，∠ACB=90°， ∴HF∥BC， ∵F是AB的中点， ∴HF=1/2BC， ∵BC=1/2AB，AB=BD， ∴HF=1/4BD，故④说法正确； ∵AD=BD，BF=AF， ∴∠DFB=90°，∠BDF=30°， ∵∠FAE=∠BAC+∠CAE=90°， ∴∠DFB=∠EAF， ∵EF⊥AC， ∴∠AEF=30°， ∴∠BDF=∠AEF， ∴△DBF≌△EFA（AAS）， ∴AE=DF， ∵FE=AB， ∴四边形ADFE为平行四边形， ∵AE≠EF， ∴四边形ADFE不是菱形； 故②说法不正确； ∴AG=1/2AF， ∴AG=1/4AB， ∵AD=AB， 则AD=4AG，故③说法正确， 故答案为①③④．