如图，在△ABC中，AC=BC＞AB
未命名 | 2015年05月05日09:32:59 | 阅读：453 | 评论：0
简介：
如图，在△ABC中，AC=BC＞AB，点P为△ABC所在平面内一点，且点P与△ABC的任意两个顶点构成△PAB，△PBC，△PAC均是等腰三角形，则满足上述条件的所有点P的个数为 （）个．
如图，在△ABC中，AC=BC＞AB，点P为△ABC所在平面内一点，且点P与△ABC的任意两个顶点构成△PAB，△PBC，△PAC均是等腰三角形，则满足上述条件的所有点P的个数为 （）个．
解：如图所示，作AB的垂直平分线，①△ABC的外心P1为满足条件的一个点，
②以点C为圆心，以AC长为半径画圆，P2、P3为满足条件的点，
③分别以点A、B为圆心，以AC长为半径画圆，P4为满足条件的点，
④分别以点A、B为圆心，以AB长为半径画圆，P5、P6为满足条件的点，
综上所述，满足条件的所有点P的个数为6．
故答案为：6．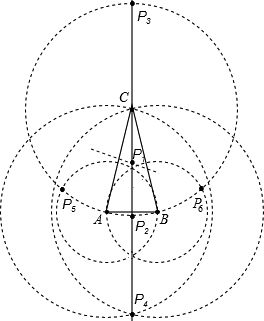
温馨提示：本文是作者 panpan39 的原创文章，转载请注明出处和附带本文链接！
相关文章
网友点评
本文暂无评论 - 欢迎您
六班网
www.6ban.cn
- 最近发表
- 标签列表
- 搜索
