panpan39

文章 987 篇 | 评论 445 次

温馨提示：该用户暂未填写个人签名！

置顶返璞归真，回归本质才是真正为孩子

      学校因为上级要求每周开展了5节体育课，上下午各开设了20多分钟大课间，又要求所有行政老师都去陪学生。      这种做法真心不能苟同。    &nb

置顶无人扶我青云志，我自踏雪至山巅-本学期小结

        转眼一学期已过了，本学期接手两个数学基础问题较多的班级，从接手的平均40多分，尤其八2七年级基础知识最高分104分的七年级的基础上，尤其本学期面对一周仅仅5节数学课的情况下，高效的让两

写给刚上高中同学--初高中各学科知识衔接方法

初中升高中，在学业上是重大的转折。新生们如何做好各门功课的衔接至关重要，所以要提前有正确的认知，才能更好地去实施。 一. 高中数学与初中数学的不同之处 1、高中数学内容抽象性、理论性更强，尤其是在高一代数中，首先碰到的就是理论性很强的函

雾霾天气影响着我国北方中东部地区

雾霾天气影响着我国北方中东部地区，给人们的健康带来严重的危害．为了让人们对雾霾有所了解．摄影师张超通过显微镜，将空气中细小的霾颗粒放大1000倍，发现这些霾颗粒平均直径为10微米〜20微米，其中20微米（1米=1000000微米）用科学记数

甲仓库储粮35吨,乙仓库储粮19吨,现调粮食15吨,应分配给两仓库各多少吨,才能使得甲仓库的粮食数量是乙仓库的两倍?

可以设需要往甲仓库中调粮X吨,则往乙仓库中调粮为（15－X）吨, 则可根据要求列方程为 35+X=2（19+15－X） 35+X=68－2X 3X＝33 X＝11 所以应该向甲仓库中调粮11吨,向乙仓库中调粮15－11＝4吨,就

我国云南、贵州等西南地区遇到旱灾,为及时灌溉农田

今年春季,我国云南、贵州等西南地区遇到旱灾,为及时灌溉农田,丰收农机公司决定支援上坪村甲乙丙三种不同功率柴油发电机共10台（每种至少一台）及配套相同型号抽水机4台、3台、2台,每 今年春季,我国云南、贵州等西南地区遇到旱灾,为及时灌溉农田

已知a^4+b^4+2a²b²-(a²+b²)-6=0,求a²+b²的值关于x的一元二次方程x²+2(m-3)x+m²=2有两个不相等的实数根,且两根的绝对值是直角三角形ABC的两直角边的长,斜边长为4倍根号6

已知a^4+b^4+2a²b²-(a²+b²)-6=0,求a²+b²的值 关于x的一元二次方程x²+2(m-3)x+m²=2有两个不相等的实数根,且两根的绝对值是直角三角形ABC的两直角边的长,斜边长为4倍根号6.求丨x1/x2丨+丨x2

最高的与最矮的

　班上有64位同学，身高都有一些微小差异。让他们排成8行8列的方阵。如果从每一行8位同学中挑出一位最高的，那么在挑出的8位同学中一定有一位最矮的同学A。让这些同学回到各自原来的位置站好后，再从每一列8位同学中挑出一位最矮的，那么在挑出的8位

以常考题为主：事半功倍的高考数学复习模式

很多考生尽管花了相当多的时间和精力，但是收效甚微，甚至由此认为高中数学很难学。如果能够转变一下复习思路，相信一定可以柳暗花明。 这个话题其实很大，篇幅限制只能和考生探讨一下以题型为主线去复习的必要性。 初次学习和再次复习不同。绝

如果一个三角形的周长等于18cm,其中两边分别是第三条边的1.5倍和3倍,这三条边长分别为

设第三边是x,另外两边是1.5x,3x 因为x+1.5x+3x=18 x=36/11 1.5x=54/11 3x=108/11 所以三别分别是36/11,54/11,108/11.

初中数学学习方法：那如何才能学好数学呢？

　　一、制定切实可行的计划，家长与孩子一起讨论，合理的罗列出完成某些要事的时间段及要达到的目标。 　　二、数学学习过程中，要有一个清醒的复习意识，逐渐养成良好的复习习惯，从而逐步学会学习。数学复习是一个反思性学习过程。要反思对所学习的知识

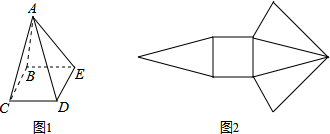
将图1的正四角锥ABCDE沿着其中的四个边剪开后

将图1的正四角锥ABCDE沿着其中的四个边剪开后，形成的展开图为图2．判断下列哪一个选项中的四个边可为此四个边？（　　） A．AC、AD、BC、DE B．AB、BE、DE、CD C．AC、BC、AE、DE D．A